Dev Log 3: AABB tree implementation (part2)

In this post I'll be talking about the concept of AABB tree and giving some hints about it's implementation.

What is an AABB tree?

In it's roots it work like any binary tree, any node has two children or none and a parent or none. Additionally every node has an AABB.

The balance of the tree becomes a little tricky. In a binary tree we balance according to the inserted number, in this case we balance according to the volume of the inserted aabb and how it affects to its new parent node.

AABBTree methods

In this section I explain the methods of the aabb tree, only add/insert and update so far because I dont need deletion right now. Later I will post about deletion.

Add/Insert method

When you insert the aabb you have to create a node for the aabb and then look for where to put the node. There are 3 scenarios and we are gonna analize the last 2.

1. The node is the first so it becomes the root of the tree.

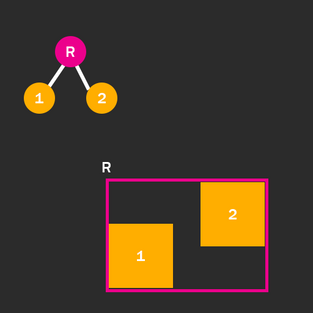
2. The node is the second to be added.

3. The node is the third+ to be added.

Blue: First node; Green: insertedNode; Pink:new root

2) As you see in the image at the right, we need to create a new node containing the two AABBs so the pseudo code looks like this.

node = new Node(); node.left = root; node.right = insertedNode; node.aabb = Union(root.aabb, insertedNode.aabb); root = parentNode;

3) This is the tricky scenario because we need to check where the inserted node will make less difference. I think this would make more sense with the pseudocode.

unionLeft = Union(nodeLeft.aabb, insertedNode) unionRight = Union(nodeRight.aabb, insertedNode) if (unionLeft.volume > unionRight.volume) Insert on right branch else Insert on left banch

Update the tree

This method consist in two parts:

1. Define what nodes are now invalid.

2. Delete de links of Invalid nodes and reinsert them.

1) This rise a question. What is an invalid node?. An invalid node is the one that is no longer contained by its parent. So the way you check this is:

if (!node.parent.aabb.contains(node.aabb)) invalid_nodes.add(node);

You can make a performance improvement by having the branch node aabb (the node that have children) to be slightly bigger that it should giving more freedom to the childrens so there is less invalid nodes per frame.

2) To delete the invalid node we need to get its parent, delete it, place its sibling into its parent place and finally delete the invalid node. In pseudo code:

parent = inv_node.parent; sibling = (parent.right == inv_node) ? parent.left : parent.right; parentPlace = GrandPa.right == parent ? &GrandPa.left : GrandPa.right; parentPlace = sibling; delete parent; delete inv:node;

Of course there need to be some check for existance since the node can have no parent wich is a more simple case. Well that's it for this post, folks. Bye!